Sorting algorithms

Various ways of sorting methods

28 Jun 2016 View Comments
#algorithm #sort #computer #complexity #merge #quick #bubble #selection #insertion #shell #counting #bucket #radix #tim #heap

So today I felt like to talk about general sorting algorithms these days. There are many sorting algorithms available, from brute force to divide and conquer. Let’s have a look at some worst time coplexity ones to better ones. For simplicity of description below, let’s assume we are sorting ascending order of integer. This can be easily applied to descending or strings depending on the requirements.

Merge Sort

• Code Example

Here is a fundamental of divide and conquer sorting algorithm which uses a comparison-based sorting method. The algorithm is stable meaning the order of sorted elements are preserved. Merge sort divides elements recursively into a smaller pieces and slowly sort them as they merges together. The amazing part of this algorithm is that it has Best/Average/Worst case performance of all O(nlogn). The pitfall of merge sort is the space complexity which is O(n). This is not the best algorithm for places where space is limited such as embbed software.

Quick Sort

an example of quicksort

• Code Example

The quick sort algorithm is famous for its recursivities and its probably the most famous sorting algorithms of all. There is no doubt a lot of people have misconception that this is the fastest algorithm out there. However, in worst case scenario, the algorithm can produce time complexity of O(\(n^2\)) when array is already sorted and pivot chosen at the last element or simply all elements in array is identical. Algorithm partitions array so element on left side has less than the element or right side has greater than equal to the element. Then algorithm recursives calls this until all element found the right position where it needs to be.

Bubble Sort

• Code Example

The bubble sort is quite old and fundametal algorithm which is discovered in 1960s. This sorting method takes each values adjacent to each other and compares and swap if one is less than the other. Worst and Average time of this sorting method is O(\(n^2\)). However, if the list is already sorted, the best time of this sort would be done in one pass which is O(n). Another variation of this sort is Odd-Even sort which is just bubble sort in parallel.

Selection Sort

• Code Example

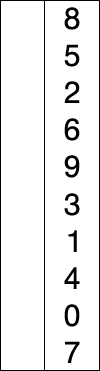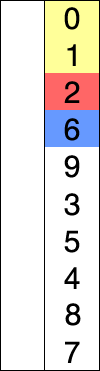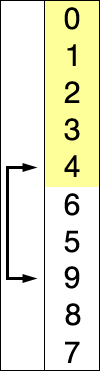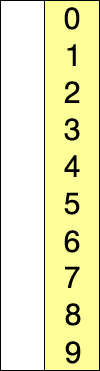
Selection sort selects the lowest in the array and places in front. Worst and Average time of this sorting method is kind of obvious, O(\(n^2\)). In order to run this sorting method, you need to run one pass, one pass -1, one pass -2, …etc. Also note, regardless of array already sorted, it needs take an effort to ensure the lowest item is in front. There are multiple variation of this method to improve the performance. For variants and further analysis, see: https://en.wikipedia.org/wiki/Selection_sort.

Insertion Sort

• Code Example

The most popular and simplest sort of all. Insertion sort goes through the array look for the position of an item that is being looked at. For example, let’s say you have 4,2,3,1. Then insertion sort will first compare 4,2 and they need to swap. List becomes 2,4,3,1. Then 4,3 will be looked at and list becomes 2,3,4,1. then it sees 2 is less then 3, leave it be. Then 4,1 will be looked at and 2,3,1,4 but 1 is still less then 3, so it swaps 3,1 -> 2,1,3,4 -> then eventually 1,2,3,4. The worst/average case of this method is O(\(n^2\)). However, the best case obviously will be O(n), simply when array is already sorted it has all the items at the position it needs to be. There are variations to this sort as well. Such as shell sort, binary insertion sort, etc. This works great when array is mostly sorted which means # of swaps it does will be significant smaller.

Shell sort

The shell sort is variation of insertion sort. You start with x-number apart and sort and narrows for each iteration and takes advantage of how fast already sorted elements works in insertion sort.

Counting Sort

• Code Example

Non-comparative sorting algorithm, which can sort better than O(nlogn) since no comparison. Downside of this sort is that we need to know # of occurrences on all numbers in an array before hand. You sort by the number of occurrence for such # in an array.

Bucket Sort

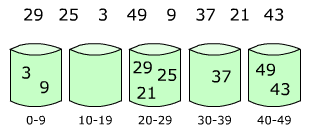Elements are distributed among bins	Then, elements are sorted within each bin

Bucket sort gathers elements inside a bucket like the diagram above. Require the number of buckets. Scatter: Go over the original array, putting each object in its bucket. Sort each non-empty bucket using any existing sorting algorithm (insertion sort used mostly). Gather: Visit the buckets in order and put all elements back into the original array. Bucket sort is unique that it has best and average time complexity of O(n+k) where k is number of buckets. However, its worst case is O(\(n^2\)) which is possible when all of elements goes into one bucket. Then this is same thing as any other sorting algorithm.

• Total Time
  1. O(n) - “Observe” input data
  2. O(k) - create and initialize buckets
  3. O(n) - first counting pass
  4. O(k) - create cumulative array(sum)
  5. O(n) - populate the output array

so end total time is O(n + k)

Radix Sort

Non-comparative integer sorting algorithm by sorting the least significant digit and next digit and so on until most significant digit is reached. Important to note here the algorithm requires single pass over the data. This algorithm is similar to bucket sort that it creates buckets of digit-position and sorts it that way. There is other ways such as using the queues or using the most significant digits first (unstable)

Tim Sort

Tim sort is a hybrid sorting algorithm that uses both binary insertion sort and merge sort. Currently, Java 7 SDK implements timsort and a new quicksort variant. Also Tim sort is default for Python, Android, GNU Octave etc. Tim sort produces good time complexity for a big number of n. Best Case: O(n) Average Case: O(nlogn) Worst Case: O(nlogn). The algorithm is stable + faster than old mergesort. If you need stable sorting method, use Tim Sort over Quicksort. Best case achieved when the input is already sorted. Worst is when they are not.

Heap Sort

• Code Example

This comparison-based unstable sorting algorithm takes an advantage of the tree being max/min heap. Taking root element and places in a sorted array. The sorting can happen in 4 stages. 1. buildMaxHeap() in O(n). 2. Swap first (root) with last child. 3. siftDown() to keep heap property in O(logn). 4. Keep repeat of 2 and 3 until all element is gone and all sorted in sorted array. Performance is O(n+n*log(n)) which is O(nlogn) for a big number of n.

Stable Sort

Stable sort is not an algorithm of sorting an array. Stable sorting algorithms maintain the relative order of records with equal keys, unstable sorting not. Anyway, I thought I would include this in here to note some of the sorting methods that are stable vs not stable.

• Well known Stable
  1. Bucket sort
  2. Bubble sort
  3. Counting sort
  4. Insertion sort
  5. Radix sort
  6. Merge sort
  7. Tim sort
• Well known unstable
  1. Quicksort
  2. Heap sort
  3. Selection sort

---