Binary Arithmetic

Elementary arithmetic operations in 0 and 1

17 Feb 2018 View Comments
#binary #arithmetic #addition #subtraction #multiplication #division

Arithmetic basically is a calculation with numbers. It is just one branch of mathematics. When you add, subtract, multiply, divide, take square roots, and so on, you are doing arithmetic. There are a couple of other branches of mathematics. For example, when you solve an equation, you are doing algebra. When you are calculating angles, areas or even modelling, you are doing geometry. Arithmetic is something you would have learned as soon as you went to the elementary school. We would have learned this as a decimal number which uses 10 digits. We are quite familiar with the base 10 arithmetic. What is 9+2? 11. What is 5*9? 45. What is 10/2? 5 What is 15-7? 8. and so on.

We can basically apply the same logic (as in decimal) to the binary numbers using 2 digits instead of 10 digits. A similar idea is taken and the best part is that they are simpler than 10 digits. So simple that sometimes we confuse because we are so accustomed to the base 10 arithmetic.

Binary Addition

Addition in binary is the easiest yet the most important process of all. The process, as I mentioned, is a lot simpler than decimal because we only have to deal with 2 digits instead of 10 digits. Binary addition sometimes is easier by calculation using the possibility table. This table is simple but handy as there are certain limited operations using the binary (0 and 1):

• 0 + 0 = 0
• 1 + 0 = 1 or 0 + 1 = 1
• 1 + 1 = 2 which is 10 in binary which is 0 with a carry of 1
• 1 + 1 + 1 (carry) = 3 which is 11 in binary which is 1 with a carry of 1

In Binary, it is represented either 0 or 1. So when we have a result larger than 1, the carry occurs since we already reached the maximum representable digit. When we deal with decimal, carry happens every 10 which is why we have 10 after 9 then it restarts from 1 like 11, 12 … etc.

Here is an example:

Addition in binary digits

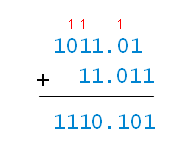Well above example has chaining carries which eventually has 1 in the 2nd column of the digit. Notice how you can apply the same logic to the decimal places.

It is definitely possible to add more than 2 binary numbers in one go. My suggestion, however, is that you add the 1st and 2nd numbers together to get the result. Then take that result and add the 3rd number to that to get another result. Then take that result and add the 4th to get another result, and continue operating until you have your answer. This way you wouldn’t get unmanageable carries since you can treat of each addition separately.

Binary Subtraction

Binary Subtraction is usually more difficult to calculate than the addition. Instead of Carrying forward (like in addition), we are going to use the term, borrowing backward for the subtraction. It is pretty straightforward when you think about it. Just remember what we are borrowing and how we use the value in the rest of the subtraction. Similar to the addition, we have a possibility table:

• 0 - 0 = 0
• 1 - 0 = 1
• 1 - 1 = 0
• 0 - 1 we borrow 1 from the before column. This makes it 10 - 1 which is 1.

You really need to remember how things are borrowed in subtraction. Let’s make things really simple, say we have 100 - 1:

1. Column 1 (rightmost) is 0. When subtracting 0 - 1, we need to borrow a 1 for the before column (Column 2).
2. Column 2 is 0 as well. We cannot give 1 to the Column 1, we would need to borrow a 1 from the Column 3 (leftmost) and which gives 10 (2 in decimal).
3. Now we can lend 1 to the Column 1 from 10 (2 in decimal). So we give one, and Column 2 is left with 1 remaining.
4. Column 1 now gotten 10 from Column 2, 10 - 1 = 1, so end result is 011.

We can verify our result by converting the binary to decimal and do the subtraction: binary 100 is 4 in decimal and binary 1 is 1 in decimal. 4-1 = 3. The result is 011 which is 3 in decimal.

Computers do not use this method though as this is not the most efficient way for a computer to subtract. They subtract by adding complements. To handle the subtraction, in decimal, you would use nine’s complement or ten’s complement; in binary, you would use ones’ complement or two’s complement.

Binary Multiplication

As you are probably familiar, we kind of memorize the “multiplication table” for the decimal from 0 to 9. So when we say what is 4x8? we know its 32 right away. Here we have 4 as the multiplicand and 8 as a multiplier.

Whenever binary multiplication is done, it is much simpler than decimal multiplication. It is basically dealing with 0 and 1 as well and the table can be made even simpler than the previous 2 operations:

• 0 * 0 = 0
• 0 * 1 = 0
• 1 * 0 = 0
• 1 * 1 = 1

For binary multiplication, I think of a AND gate operation. It is really simple if you think this way. One is true, one is false. You’ll notice two things: there are never any carries, and the result is either 0 or 1.

We can start with an example:

Multiplication in binary digits

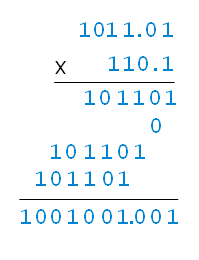As you can see it is similar to how we deal with decimal multiplication except that its just within 0 or 1. This is simpler by folds than the decimal multiplication.

Binary Division

Well, as you may have guessed, the binary division is simpler than decimal division. Remember when you work on a simple division, what dividend, divisor and quotient is? To recap, see the image below for what they are as I will be describing the division with these terms.

Explaining what quotient, divisor, dividend are in division

Similar to the decimal division, you will need to find out how many divisors can divide the dividend to get the partial quotient. Let’s just dive straight into the example:

As usual, let’s start off with an example:

Division in binary digits

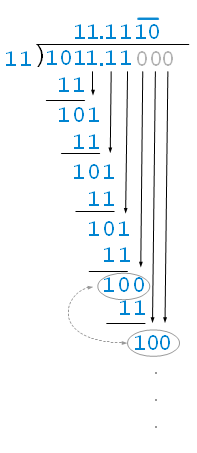We have 11 as the divisor, 1011.11 as the dividend. Let’s solve this step by step.

1. Can 11 fit into the first 1 of the 1011.11 (dividend)? Nope, so we get 0 as a first digit of the quotient.
2. Can 11 fit into the first and second 10 of the 1011.11? Nope, so we still get 0 as the second digit of the quotient.
3. Can 11 fit into the first 3 digits of the dividend which is the 101? Yes, so we get 1 as the third digit of the quotient.
4. Subtracting the 11 from the 101, we get 10, then we bring the next 1 down to make 101 and there we can fit in 11. and the fourth digit of the quotient becomes 1.
5. We keep following the similar logic in the picture above to achieve our quotient of 0011.11101010… Note how 10 keeps repeating because the division keeps repeating like the decimal.

---