Nash Equilibrium
Basic Game Theory that everyone should know
10 Jun 2017
View Comments
#nash
#equilibrium
#computer
#game
#theory
A Nash equilibrium is a set of mutual best responses: each person is doing the best to what everyone else is doing. Finding the balance is the key. There will be a point where each individual won’t change their choices in a game.
In a game like rock-scissors-paper where Nash equilibrium would just be “to randomize” since each play has the same weight. Here is what I mean. Let’s say that you want to play rock. However, your opponent might think that you will play the rock that he is playing the paper. However, you might think that your opponent might think that you will play the rock that he is playing the paper that you will play the scissor instead. This is often called infinite recursion (with no base case) in computing science which often times do not have a winning strategy. Randomizing your play is the mutual best responses each can play.
Below is the film, “A Beautiful Mind”, based on Dr. Nash’s life which tries to explain game theory in a scene in which Russell Crowe, playing Dr. Nash, is at a bar with three friends, and they are all enraptured by a beautiful blond woman who walks in with four brunette friends. This event portrayed by Crowe is not likely to happen in real life as there are many other considerations you need to achieve the goal of “dating with a girl”. But it certainly is a game theory that can have an equlibrium as well.
Let’s look at some of the examples of Nash equilibrium and hopefully the concept is clearer at the end.
Basic Examples
Prisoner’s dilemma
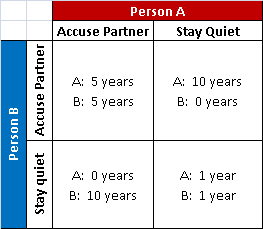
The prisoner’s dilemma is a game analyzed by game theory. It was initially devised around 1950. There are many versions of the prisoner’s dilemma, but generally following is how it is played (see the 2x2 matrix on the left for better understanding): There is a situation where two (to make the problem simpler) people who have been captured to confess their crimes. You are isolated from each other and put into a separate room. The prosecutor walks in for each one and makes a bargain to them by making following offers:
- If A and B both confess, each of them serves 5 years in prison
- If A tells on B, but B remains silent, A will be set free and B will serve 10 years in prison (and vice versa)
- If A and B both remain silent (stay quiet), both of them will only serve 1 year in prison (there is not enough evidence)
The ‘dilemma’ faced by the prisoners here is that, whatever the other does, each is better off “confess” than remaining silent. There is a unique equilibrium point by “confess” which would be the optimal choice to what the other is doing.
- Usage in real life
Let’s watch the following clip which portrays the dilemma in reality. It isn’t exactly like the situation described above since the contestants are put in the same room and able to chat each other before making the choice.
Chicken Game

This game is similar to the Prisoner’s dilemma in that we have a similar 2x2 matrix, but there is a key difference. Here we have 2 Nash equilibria (mixed strategies) instead of a single one (pure strategy). The principle of the game is that while it is to both players’ benefit if one player yields, the other player’s optimal choice depends on what his opponent is doing. If we try to find out the Nash equilibrium, we find that there are 2: when his opponent yields, the player should not, but if the opponent fails to yield, the player should. This is called mixed strategy Nash equlibrium. The Nash equilibria in this scenario are Continue Straight/Swerve and Swerve/Continue Straight.
- Usage in real life
The negotiations between Greece and the Eurozone financial chiefs represent a typical game of ‘Chicken’. As in the game of Chicken, both Greece and the Eurozone (Germany mostly) have the option to make concessions (Swerve) or hold firm in negotiations (Drive Straight). If Greece believes the Eurozone will make concessions, it will achieve the best outcome by standing firm; if it believes the Eurozone will stand firm in negotiations, it’s the best option is to make concessions to avoid the dire consequences of a full-blown default (and vice-versa). I am sure you will come across an example of the “chicken” game in life often.
