Fibonacci Numbers
28 Dec 2016
View Comments
#computer
#dynamic
#programming
#algorithm
#recursion
#Fibonacci
#sequence

What Are Fibonacci Numbers?
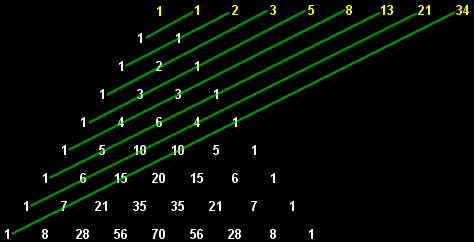
Fibonacci numbers follow integer sequence that every number after the first two is the sum of the two preceding ones like following: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. and so on. Each number is basically the sum of the previous two. To show you this in a simple mathematic equation, it is represented as F(1) = F(2) = 1 , Fn = Fn-1 + Fn-2. In modern usage, the equation could be extended to include F(0) = 0. The sequence is named after Leonardo Bonacci (also known as “Fibonacci” 1170-1250)—was an Italian mathematician, who is considered to be “the most talented Western mathematician of the Middle Ages”. You could find Fibonacci happening in many places. You would be quite surprised to see how frequent Fibonacci sequence appears throughout our life. Fibonacci is also pretty common in mathematics. Let’s take a look at the below illustration which shows Fibonacci sequence found in Pascal’s Triangle:
Usages in Math/Science/Nature
1) Fibonacci numbers are also used in planning poker, which is a step in estimating in software development projects that use the Scrum (software development) methodology. If you are working in a software firm, you would have noticed Fibonacci numbers are being used to estimate stories/features in the planning.
2) Fibonacci numbers are used as a prediction to the stock trading. The most notable relationship can be found by dividing one Fibonacci number by the next one in the series, which will give you the “Golden Ratio” of 0.618. Golden ratios and Fibonacci have the fairly close relationship. There are many interesting articles online regarding this. Honestly, I do not know much about this as I am not a stock broker :p
3) Fibonacci search technique which is similar to the binary search algorithm uses the fibonacci sequence to find an item. Compared to binary search where the sorted array is divided into two arrays which are then examined recursively. Fibonacci search only examines locations whose addresses have lower dispersion. It means when the time needed to access a storage location varies depending on the location accessed, this algorithm may have an advantage since accessing an element in an array is not uniform.
4) Fibonacci is also found in many natures. I would strongly advise you search for nature and Fibonacci. It is truly amazing how it follows this pattern in real life. Especially I found it really fascinating when I read the examples on fibonacci and bees or variety of other events such as petal count which is discussed here
Performance Considerations
There is way to compute Fibonacci numbers in a program. Today I would like to show examples with Python. Anyways, here is one of the simplest but slow algorithms would be using a regular recursion to solve Fibonacci,
def fib(self, n):
if n == 0: return 0
elif n == 1: return 1
else: return self.fib(n-1)+self.fib(n-2)This method creates recursion until one of two base condition is met. Well, frankly, this method is probably the worst possible way to solve the Fibonacci problem. Recursion method is usually bad in performance unless the solution cannot be solved using iteratively. Here is an iterative solution that solves above recursion, reason is explained below but let’s take a look at the iterative example first:
def fib2(self, n):
if (n == 1 or n == 2):
return 1
n0 = 1
n1 = 1
for i in range(2, n):
temp = n1
n1 += n0
n0 = temp
return n1This method is much better as it does not store the call into the stack. In the recursive version, it is creating functions recursively which is expensive because function call involves pushing values into stacks while iterative method operates on the same stack with exact # of times it tells it to perform. I ran above algorithms with fib(35) vs fib2(35) in my computer which took --- 4.92036604881 seconds --- with recursion and --- 0.000201940536499 seconds --- with iterative solution. Performance suffers really bad after this for recursion method. With fib(40), it took --- 55.7830410004 seconds --- with recursion. Amazingly, with fib2(40) it only took --- 0.000519037246704 seconds --- for the iterative solution.
Then I asked this question myself… Is it anything to do with the recursion itself? Answer is not really. Look closely to the following recursion+dynamic programming (cached, memoization) which runs so much faster.
table = [0, 1]
def fib3(self, n):
if (0 <= n < len(self.table)):
return self.table[n]
self.table.append(self.fib3(n - 1) + self.fib3(n - 2));
return self.table[n]Why is this? Above algorithm runs — 0.000197887420654 seconds — for fib3(35) and — 0.000597953796387 seconds — for fib3(40) which pretty much is comparable to the iterative solution (fib2). The fib3 method is essentially a top-down approach for dynamic programming. When you measure the number of times the item is being looked at to calculate the Fibonacci, Iterative and DP is essentially the same. Let me show you with examples what I mean.
I ran little experiments to see what exactly is going on here. So with a regular recursion that called fib(5), it called the function itself 15 times. However, with Dynamic Programming ways (caches/memoization), it ran 9 times. Literally, all DP had to perform was to recurse in and recurse out as it uses the cached values on intermediate values. The intermediate calls do not need to recurse down to base condition again which is a huge saving here. This example is only called with n=5, a number of functions calls will be significantly different as n grows. With just fib(10), regular recursive method ran 177 times vs 19 times for DP recursion. Now you can imagine what would happen when input size n grows even larger. I am satisfied with the result which depicts why regular recursion is so much slower than iterative/DP solution. Well, the key comparison between algorithms were just # of times code gets executed.
By the way, here is the link to the source of Python Fibonacci examples.
